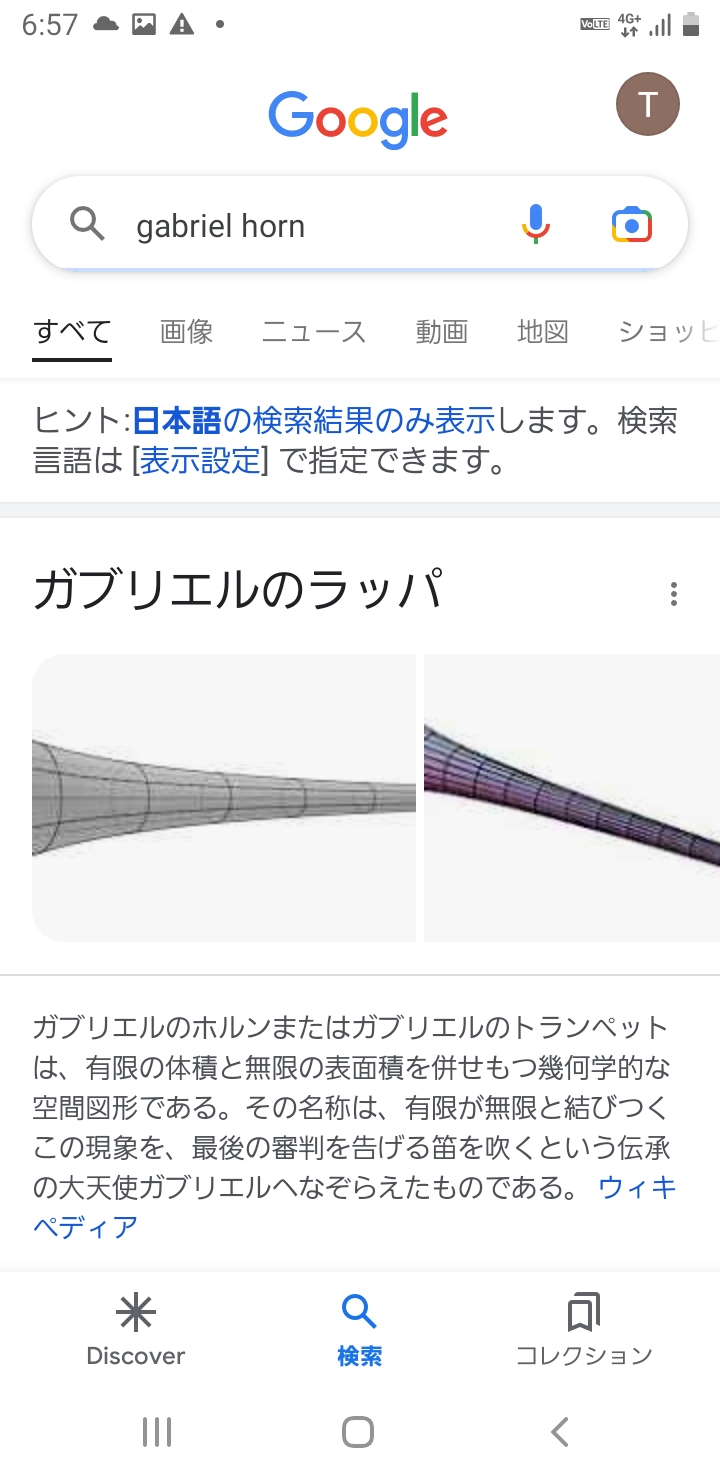
ガブリエルのラッパ
y=1/xのx軸回転対称図形を考える。
どうでもいい話だがスタートはx≧1とする。
無限遠までの図形を考える。
体積は、
dV=πR^2・dx=π/x^2・dxなので
体積分はπになる。
この図形の表面積は無限大になる、
なぜなら微小表面積が
dS
=2π(y+y+dy)/2・dx
≧2πy・dx
∝1/x・dx
であるからである。
このように、y=1/x回転体を「ガブリエルのラッパ」とよひ、
この図形は体積が有限で表面積が無限大なのである。
🐻ガブリエルのラッパは体積が有限で表面積が無限大の立体図形である。